АВТО БЛОГ YAMAHA-VOLGA.RU

Как работает дифференциал нестерова: Срок регистрации домена blokirovka-dan.ru истёк

9 ноября, 1970 by admin

Самоблокирующийся дифференциал: принцип действия

Термин «блокировка дифференциала», или «самоблокирующейся дифференциал» (самоблок), слышали многие автомобилисты, а вот как этот процесс выглядит на практике, знают лишь некоторые. И если раньше такой «опцией» автопроизводители оборудовали преимущественно внедорожники, то сейчас ее можно встретить и на вполне городском автомобиле. Кроме того, зачастую владельцы машин не оборудованных самоблоками, поняв, какую пользу они приносят, устанавливают их самостоятельно.

Но прежде чем разбираться с тем, как работает самоблокирующийся дифференциал, нужно понять, как он функционирует без блокировки.

Что такое дифференциал

Дифференциал (дифф) по праву можно считать одним из главных элементов конструкции трансмиссии автомобиля. С его помощью происходит передача, изменение, а также распределение выдаваемого двигателем крутящего момента между парой потребителей: колесами, расположенными на одной оси машины или же между ее мостами. Причем сила потока распределяемой энергии при необходимости может быть различной, а значит, и скорость вращения колес — разной.

В трансмиссии автомобиля дифф может быть установлен: в картере заднего моста, КПП и в раздаточной коробке, в зависимости от устройства привода(ов).

Те диффы, которые установлены в мосту или КПП, называются межколесными, а который находится между осями машины, соответственно – межосевым.

Назначение дифференциала

Как известно, автомобиль во время движения совершает различные маневры: повороты, перестроения, обгоны и т. д. Кроме того, поверхность дороги может содержать неровности, а это значит, что колеса автомобиля, в зависимости от ситуации, в одно и то же время могут проходить различное расстояние. Поэтому, например, при повороте, если скорость вращения колес на оси будет одинаковой, то одно из них неминуемо станет пробуксовывать, что приведет к ускоренному износу покрышек. Но это не самое страшное. Гораздо хуже то, что у транспортного средства значительно снижается управляемость.

Вот для решения подобных проблем и придумали дифференциал – механизм, который будет перераспределять энергию, поступающую от двигателя, между осями автомобиля в соответствии с величиной сопротивления качению: чем оно меньше, тем больше будет скорость вращения колеса, и наоборот.

Механизм дифференциала

На сегодняшний день существует множество разновидностей диффов, и их устройство довольно сложное. Однако принцип работы в целом одинаков, поэтому будет проще для понимания рассмотреть самый простой тип – открытый дифференциал, который состоит из следующих элементов:

1. Шестеренок, закрепленных на полуосях.
2. Ведомой (коронной) шестерни, выполненной в виде усеченного конуса.
3. Ведущей шестерни, закрепленной на конце ведущего вала, которая в совокупности с коронной образует главную передачу. Так как ведомая шестерня по размерам больше ведущей, то последней придется сделать несколько оборотов вокруг своей оси, прежде чем коронная выполнит только один. Следовательно, именно эти два элемента дифференциала снижают величину энергии (скорости), которая в итоге дойдет до колес.
4. Сателлитов, которые образуют планетарный механизм, играющий ключевую роль в обеспечении необходимой разности в скорости вращения колес.
5. Корпуса.

Как работает дифференциал

Во время прямолинейного движения автомобиля его полуоси, а значит, и колеса, вращаются с такой же скоростью, как и ведущий вал со своей косозубой шестерней. Но во время поворота воздействующая нагрузка на колеса становится различной (одно из них пытается крутиться быстрей), и за счет этой разницы освобождаются сателлиты. Теперь энергия двигателя проходит через них, а так как пара сателлитов – это две отдельные, независимые шестерни, то к полуосям передается разная по величине частота вращения. Таким образом, мощность, вырабатываемая двигателем, распределяется между колесами, но неравномерно, а в зависимости от действующей на них нагрузки: то, что двигается по внешнему радиусу, испытывает меньшее сопротивление качению, поэтому дифф передает на него больше энергии, раскручивая быстрее.

Разницы в том, как работает межосевой дифференциал и межколесный, нет: принцип действия аналогичен, только в первом случае распределенный крутящий момент направлен к осям автомобиля, а во втором — к его колесам, расположенным на одной оси.

Потребность в межосевом диффе особенно становится заметна во время движения машины по пересеченной местности, когда ее вес давит на ту ось, которая находится ниже другой, например, на подъеме или спуске.

Проблема дифференциала

Несмотря на то что дифференциал, безусловно, играет большую роль в конструкции автомобиля, его работа иногда создает проблемы для водителя. А именно: когда одно из колес оказывается на скользком участке дороги (грязи, льду или снегу), то другое, находящееся на более твердом грунте, начинает испытывать повышенную нагрузку, дифф старается это исправить, перенаправляет энергию двигателя на скользящее колесо. Таким образом, выходит, что оно получает максимальное вращение, в то время как другое, имеющее плотное сцепление с грунтом, попросту остается неподвижным.

Вот именно для решения подобных проблем была придумана блокировка (отключение) дифференциала.

Принцип блокировки и ее виды

Поняв принцип работы дифференциала, можно заключить, что если заблокировать его, то увеличится крутящий момент на том колесе или оси, которое имеет лучшее сцепление. Это можно сделать, если соединить его корпус с одной из двух полуосей или же остановить вращение сателлитов.

Блокировка может быть полной – когда части дифференциала соединяются жестко. Осуществляется, как правило, при помощи кулачковой муфты и управляется водителем через специальный привод из кабины автомобиля. Или же она может быть частичной, в этом случае на колеса передается только ограниченное усилие – так работает самоблокирующийся дифференциал, которому участие человека не требуется.

Как работает самоблокирующийся дифференциал

Самоблокирующийся дифференциал, по сути, представляет собой компромисс между полным блоком и свободным диффом и позволяет снизить пробуксовку колес машины в случае возникновения между ними разницы в коэффициенте сцепления с грунтом. Таким образом, значительно повышается проходимость, управляемость на бездорожье, а также динамика разгона автомобиля, причем независимо от качества дороги.

Самоблок исключает полную блокировку колес, что защищает полуоси от критических нагрузок, которые могут возникнуть на дифференциалах с принудительным выключением.

Блокировка с полуосей снимается автоматически, если при прямолинейном движении скорости вращения колес выравнивается.

Самые распространенные типы самоблоков

Дисковый самоблок – это набор фрикционных (трущихся) дисков, установленных между корпусом диффа и шестерней полуоси.

Понять, как работает дифференциал с таким блоком, несложно: пока машина едет по прямой, корпус диффа и обе полуоси крутятся вместе, как только в скоростях вращения появляется разница (колесо попало на скользкий участок), между дисками возникает трение, снижающее ее. То есть колесо, оставшееся на твердом грунте, продолжит вращаться, а не остановится, как в случае свободного дифференциала.

Вискомуфта, или иначе вязкостная муфта, так же как и предыдущий дифф, содержит два пакета дисков, только на этот раз перфорированных, установленных между собой с небольшим зазором. Одна часть дисков имеет сцепление с корпусом, другая – с валом привода.

Диски, помещены в емкость, заполненную кремнийорганической жидкостью, которая при равномерном их вращении остается в неизменном состоянии. Как только между пакетами появляется отличие в скорости, жидкость начинает быстро и сильно густеть. Между перфорированными поверхностями возникает сопротивление. Чересчур раскрутившийся пакет таким образом притормаживается, и скорость вращения выравнивается.

Зубчатый (винтовой, червячный) самоблок. Его работа базируется на способности червячной пары расклиниваться и тем самым блокировать полуоси при возникновении на них разницы в крутящих моментах.

Кулачковый самоблок. Чтобы понять, как работает дифференциал такого типа, достаточно представить открытый дифф, в котором вместо планетарного шестеренчатого механизма установлены зубчатые (кулачковые) пары. Кулачки проворачиваются (перескакивают), когда скорости вращения колес практически одинаковы, и жестко блокируются (заклиниваются), как только какое-то из них начинает пробуксовывать.

Разницы в том, как работает блокировка межосевого дифференциала и межколесного, нет – принцип действия одинаков, отличия только в конечных точках: в первом случае – два моста, во втором – два колеса, установленных на одной оси.

Отечественная «Нива» и ее дифференциалы

В линейке отечественных ВАЗов «Нива» занимает особенное место: в отличие от своих «родственников» по конвейеру, эта машина оборудована не выключаемым полным приводом.

В трансмиссии ВАЗовского внедорожника установлено три дифференциала: межколесные – в каждом мосту, и межосевой – в раздатке. Несмотря на такое количество, разбираться заново в том, как работают дифференциалы на «Ниве», не придется. Все точно так же, как описывалось выше. То есть, во время прямолинейного движения машины, при условии отсутствия пробуксовок на колесах, тяговое усилие между ними распределено равномерно и имеет одинаковую величину.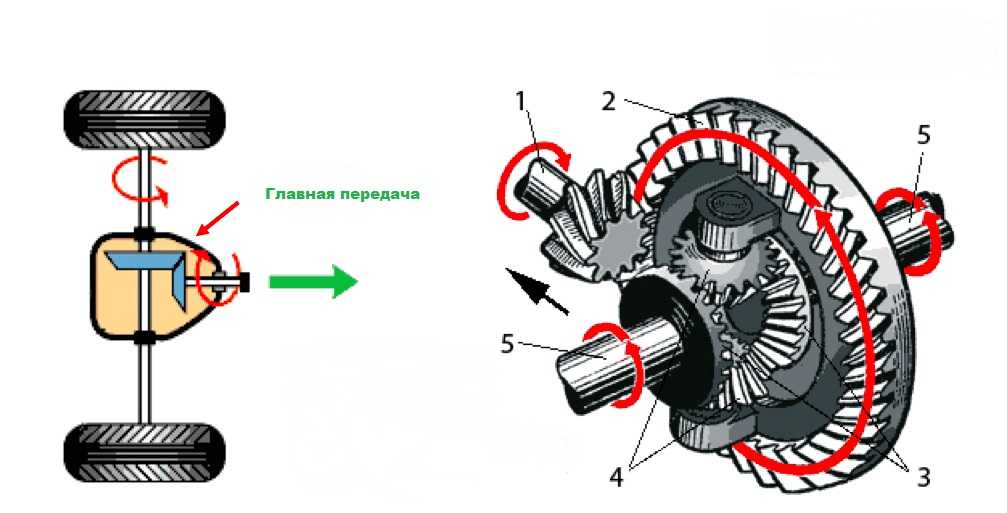 Когда какое-то из колес начинает буксовать, то вся энергия от двигателя, пройдя через диффы, направляется к этому колесу.

Блокировка дифференциалов «Нивы»

Прежде чем говорить о том, как работает блокировка дифференциалов на «Ниве», следует отметить один момент, а именно уточнить назначение передней (маленькой) ручки раздаточной коробки.

Некоторые водители полагают, что с ее помощью у машины включается передний привод – это не так: и передний, и задний приводы у «Нивы» задействованы всегда, а этой ручкой осуществляется управление дифференциалом раздатки. То есть пока она установлена в положении «вперед», дифф работает в штатном режиме, а когда «назад» – отключается.

А теперь непосредственно о блокировке: при выключении дифференциала валы раздаточной коробки замыкаются между собой муфтой, тем самым принудительно выравнивая скорости их вращения, то есть суммарная скорость колес передней оси приравнивается к суммарной скорости задней. Распределение тяги происходит в сторону большего сопротивления. Допустим, буксует заднее колесо, если включить блокировку, тяговое усилие уйдет на переднюю ось, колеса которой вытянут машину, но если одновременно с задним забуксует и переднее колесо, то самостоятельно «Нива» уже не выберется.

Чтобы такого не случалось, автолюбители в мосты устанавливают самоблоки, которые помогут вытянуть застрявшую машину. На сегодняшний день самым популярным среди владельцев «Нивы» является дифференциал Нестерова.

Самоблок Нестерова

Именно в том, как работает дифференциал Нестерова, и заключен секрет его популярности.

Конструкция дифа позволяет не только оптимально регулировать угловую скорость колес машины при совершении маневров, но и в случае пробуксовок или вывешивании колеса устройство отдает ему минимальное количество энергии от двигателя. Причем реакция самоблока на изменение дорожной ситуации практически мгновенная. Кроме того, дифференциал Нестерова значительно улучшает управляемость машины даже на скользких поворотах, повышает курсовую устойчивость, повышает динамику разгона (особенно в зимний период), снижает расход горючего. А монтаж устройства не требует никаких изменений в конструкции трансмиссии и устанавливается точно так же, как классический дифф.

Дифференциал нашел применение не только в автомобильной технике, он оказался весьма полезен и на мотоблоках, значительно облегчив жизнь его владельцам.

Дифференциал для мотоблока

Мотоблок — агрегат довольно тяжелый, и, чтобы его просто повернуть, требуется немало усилий, а при нерегулируемой угловой скорости вращения колес это становится еще сложнее. Поэтому владельцы этих машин, если диффы не предусматривались изначально конструкцией, приобретают и устанавливают их самостоятельно.

Как работает дифференциал мотоблока? По сути, он лишь обеспечивает легкий разворот машины, останавливая одно из колес.

Другая его функция никак не связанная с перераспределением мощности – это увеличение базы колес. Конструкция дифференциала предусматривает его использование как удлинителя осей, что делает мотоблок более маневренным и устойчивым к опрокидываниям, особенно на поворотах.

Словом, дифференциал – вещь весьма полезная и незаменимая, а его блокировка в разы повышает проходимость автомобиля.

Что такое самоблок

21.02.2017 08:00

Что такое самоблокирующийся червячный дифференциал?

Самоблокирующийся червячный дифференциал (самоблок) — устройство, которое позволяет частично компенсировать главный недостаток свободного дифференциала, а именно его полную беспомощность при наезде одного колеса на скользкое покрытие. По принципу работы, самоблокирующиеся дифференциалы можно разделить на два типа: speed sensitive, то есть срабатывающих от разницы в угловых скоростях вращения полуосей, и torque sensitive — срабатывающих от разницы передаваемого на полуоси крутящего момента. Для понимания работы самоблока сначала разберёмся с принципом работы обыкновенного дифференциала и его недостатками.

Дифференциал — это механическое устройство, которое передает крутящий момент с одного источника на два независимых потребителя таким образом, что угловые скорости вращения источника и обоих потребителей могут быть разными относительно друг друга.

Принцип работы обыкновенного дифференциала

Почему для этого нужен дифференциал? В любом повороте, путь колеса оси, двигающегося по короткому (внутреннему) радиусу, меньше, чем путь другого колеса той же оси, которое проходит по длинному (внешнему) радиусу. В результате этого, угловая скорость вращения внутреннего колёса должна быть меньше угловой скорости вращения внешнего колеса. В случае с не ведущим мостом, выполнить это условие достаточно просто, так как оба колеса могут не быть связанными друг с другом и вращаться независимо. Но если мост ведущий, то необходимо передавать крутящий момент одновременно на оба колеса (если передавать момент только на одно колесо, то возможность управления автомобилем по современным понятиям будет очень плохой).

При жесткой же связи колёс ведущего моста и передачи момента на единую ось обоих колёс, автомобиль не мог бы нормально поворачивать, так как колеса, имея равную угловую скорость, стремились бы пройти один и тот же путь в повороте. Дифференциал позволяет решить эту проблему: он передаёт крутящий момент на раздельные оси обоих колёс (полуоси) через свой планетарный механизм с любым соотношением угловых скоростей вращения полуосей. В результате этого, автомобиль может нормально двигаться и управляться как на прямом пути, так и в повороте.

Однако, ввиду физики устройства, у планетарного механизма есть очень нехорошее свойство: он стремится передать полученный крутящий момент туда, куда легче. Например, если оба колеса моста имеют одинаковое сцепление с дорогой и усилие, необходимое для раскручивания каждого из колёс одинаковое, дифференциал будет распределять крутящий момент равномерно между колёсами. Но стоит только появится ощутимой разнице в сцеплении колёс с дорогой (например, одно колесо попало на лёд, а другое осталось на асфальте), как дифференциал тут же начнёт перераспределять момент на то колесо, усилие для раскрутки которого наименьшее (то есть на то, которое находится на льду).

В полноприводных автомобилях дифференциалом обычно оборудованы два моста, а зачастую дифференциал можно обнаружить еще и между мостами (межосевой дифференциал). Таким образом, мы получаем схему трансмиссии, в которой присутствуют целых три дифференциала: два мостовых и один межосевой. Последний необходим для постоянного движения с полным приводом и передачей момента на все четыре колеса. Ведь в повороте колёса рулевого моста (обычно переднего) имеют совсем другие угловые скорости, нежели чем колёса заднего моста. Межосевой дифференциал призван передавать крутящий момент от коробки передач к обоим ведущим мостам с разным соотношением угловых скоростей. Такая схема с тремя дифференциалами является одной из самых распространённых схем для постоянного полного привода (Full time 4WD).

Возвращаясь к вышеописанному проблемному свойству планетарного механизма, интересно рассмотреть ситуацию, когда полноприводный автомобиль с межосевым дифференциалом одним из четырёх колёс попал на тот же лёд (или в скользкую яму). Что тогда произойдёт ? Дифференциал моста, колесо которого находится на льду, отдаст весь полученный крутящий момент на это колесо. Межосевой дифференциал, в свою очередь, тоже стремится передать крутящий момент туда, куда легче. Естественно, межосевому дифференциалу легче отдать момент на мост с прокручивающимся на льду колесом, нежели чем на мост, колёса которого имеют хорошее сцепление с дорогой и могут двигать автомобиль. В результате, весь крутящий момент от двигателя и коробки передач пойдёт на раскручивание единственного колеса, находящегося на льду.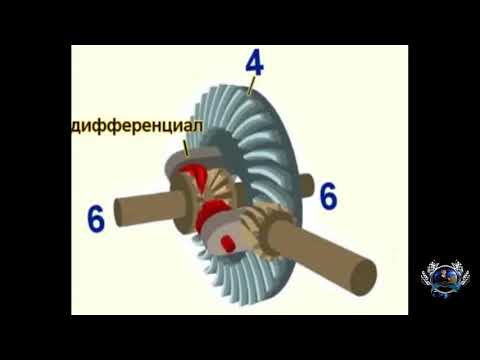

Основной целью блокировки дифференциала является передача необходимого крутящего момента обоим его потребителям (полуосям или карданам). Существуют принципиально разные методы решения данной задачи. В данном разделе мы рассмотрим способ частичной блокировки с помощью самоблокирующегося дифференциала. Другие способы частичной блокировки дифференциала можно посмотреть здесь, а с метод полной блокировки дифференциала можно ознакомится в разделе «Что такое принудительная блокировка?»

Самоблокирующийся червячный дифференциал типа «Квайф»

Автором этой конструкции является англичанин Rod Quaife. В данном случае, оси сателлитов параллельны полуосям. Сателлиты расположены в своеобразных карманах чашки дифференциала. При этом парные сателлиты имеют не прямозубое зацепление, а образуют между собой еще одну гипоидную пару, которая расклиниваясь, так же участвует в процессе блокировки.

Принцип работы cамоблокирующегося дифференциала

На рисунке приведен эскиз самоблокирующегося дифференциала. Рассмотрим его элементы и принцип работы.

Когда одно из колес (например, правое) начинает отставать, связанная с ним полуосевая шестерня 4 вращается медленнее корпуса 1 и поворачивает входящий с ней в зацепление сателлит 5. Он передает движение связанному с ним сателлиту 5 из левого ряда, а тот, в свою очередь, на левую полуосевую шестерню 3. Так обеспечиваются разные угловые скорости колес в повороте. Благодаря разности крутящих моментов на колесах в винтовом зацеплении возникают осевые и радиальные силы, прижимающие полуосевые шестерни 3, 4 и сателлиты 5, 6 торцами к корпусу 1, 2.

— Мы производим и продаем Cамоблокирующиеся дифференциалы на следующие марки и модели автомобилей:

• УАЗ
  • УАЗ 3160
  • УАЗ 31512
  • УАЗ 469
• ВАЗ
  • ЛАДА
  • НИВА
  • НИВА ШЕВРОЛЕ
• ГАЗ
  • ГАЗ 3110 и новее
  • Газель
  • Соболь
• FORD
  • Ranger
  • Maverick
• MAZDA
  • BT-50
  • BT-2500/B-2500
• SUZUKI
  • Jimny, Samurai
  • Vitara
• OPEL
  • Frontera
  • Monterey
• TAGAZ, SSANGYONG
  • TAGAZ
  • SSANGYONG
• ZX
  • Admiral
  • Landmark

• GREAT WALL
  • Hover
  • Safe
  • Deer
  • Sailor
• ISUZU
  • Amigo/Rodeo/Mu/Axiom
  • Bighorn
  • Trooper
  • Vehicross
• MITSUBISHI
  • Pajero
  • Pajero Sport, L200
  • Pajero mini
  • Pinin
• TOYOTA
  • LandCruiser 71, 76, 78, 79, 100, 105 Series, Lexus LX470
  • LandCruiser Prado, 90, 120, 150 series, Lexus GX
  • LandCruiser Prado 120, 150 series, Lexus GX
  • Bundera, LendCruiser II, LJ70, RJ70
  • HiLux Surf, Pickup, Hiace, 4Runner
  • 4Runner, LN61, YN63
  • T100, Tacoma, Tundra
  • FJ Cruiser (US)

• HYUNDAI
  • Accent
  • Elantra
  • Getz
  • i20\ i30\ i40\ix20
  • Solaris
  • Terracan 
  • Tucson\ ix35
  • Veloster
• KIA
  • Carens
  • Ceed
  • Cerato\ Forte\ K3\ Spectra
  • Mohave
  • RIO\Ih22
  • Soul
  • Sorento
  • Sportage
  • Venga
• NISSAN
  • NP-300 (Pickup)
  • Navara (Frontier)
• JEEP
  • Jeep
• RENAULT
  • Duster

Индивидуальный проект каждой блокировки разработан в нашем конструкторском бюро.

Как проектируется проходимость

Высококачественная конструкционная легированная сталь 40Х, прочная и износоустойчивая.

О качестве материалов

Каждая деталь прошла контроль качества после изготовления, обработки, и перед сборкой блокировки.

О внимании к деталям

Разработана и собрана в России.
Гарантия 1 год.

О гарантии

Ускоренная оптимизация формул PDE Framework для корпуса Active Contour

. 2020;13(4):2029-2062.

дои: 10.1137/19m1304210. Epub 2020 19 ноября.

Энтони Йеззи ¹ , Ганеш Сундамурти ² , Минас Беньямин ¹

Принадлежности

Принадлежности

• ¹ Факультет электротехники и вычислительной техники, Технологический институт Джорджии 30332 США.
• ² Исследовательский центр Raytheon Technologies.

• PMID: 34336084
• PMCID: PMC8320808
• DOI: 10.1137/19м1304210

Бесплатная статья ЧВК

Энтони Йеззи и др. SIAM J Imaging Sci. 2020.

Бесплатная статья ЧВК

. 2020;13(4):2029-2062.

дои: 10.1137/19m1304210. Epub 2020 Ноябрь 19.

Авторы

Энтони Йеззи ¹ , Ганеш Сундамурти ² , Минас Беньямин ¹

Принадлежности

• ¹ Факультет электротехники и вычислительной техники, Технологический институт Джорджии 30332 США.
• ² Исследовательский центр Raytheon Technologies.

• PMID: 34336084
• PMCID: PMC8320808
• DOI: 10.1137/19м1304210

Абстрактный

После основополагающей работы Нестерова методы ускоренной оптимизации использовались для значительного повышения производительности оценки параметров на основе градиента первого порядка в сценариях, где стратегии оптимизации второго порядка либо неприменимы, либо нецелесообразны.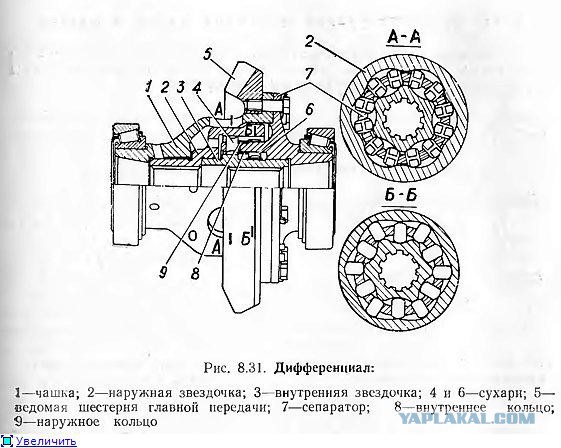 Мало того, что ускоренный градиентный спуск сходится значительно быстрее, чем традиционный градиентный спуск, он также выполняет более надежный локальный поиск в пространстве параметров, сначала выходя за пределы, а затем осциллируя обратно по мере того, как он устанавливается в окончательную конфигурацию, тем самым выбирая только локальные минимизаторы с базисом притяжения достаточно велико, чтобы сдержать начальный выброс. Такое поведение сделало методы ускоренного и стохастического градиентного поиска особенно популярными в сообществе машинного обучения. В своей недавней статье PNAS 2016 Вариационный взгляд на ускоренные методы оптимизации , Вибисоно, Уилсон и Джордан демонстрируют, как широкий класс ускоренных схем может быть представлен в вариационной структуре, сформулированной на основе дивергенции Брегмана, что приводит к континуальным предельным ОДУ. Мы показываем, как их формулировку можно распространить на бесконечномерные многообразия (начиная здесь с геометрического пространства кривых и поверхностей), заменив дивергенцию Брегмана скалярными произведениями на касательном пространстве и явно введя модель распределенной массы, которая развивается вместе с объект интереса в процессе оптимизации. Модель коэволюционирующей массы, которая введена исключительно для того, чтобы наделить оптимизацию полезной динамикой, также связывает результирующий класс ускоренных схем оптимизации на основе PDE с гидродинамическими формулировками оптимального массопереноса.

Ключевые слова: 35Б35; 35J20; 35Р30; 49М99; 53С99; 65М99; Нестеров; ускорение; градиентный спуск; коллекторы; оптимизация общественного транспорта; уравнения в частных производных; вариационный.

Цифры

Рисунок 1.

Градиенты Соболева в зависимости от регуляризации энергии.

Рисунок 1.

Градиенты Соболева в зависимости от регуляризации энергии.

Фигура 1.

Градиенты Соболева в зависимости от регуляризации энергии.

Рисунок 2.

Интерпретация физики ускоренного спуска.

Рисунок 2.

Физическая интерпретация ускоренного спуска.

Интерпретация физики ускоренного спуска.

Рисунок 3.

Различные начальные контуры, переходящие в…

Рисунок 3.

Различные начальные контуры, перетекающие в локальные минимизаторы энергии.

Различные начальные контуры перетекают в локальные минимизаторы энергии.

Рисунок 4.

Ускоренное обтекание активных контуров…

Рисунок 4.

Ускоренные активные контуры, обтекающие локальные минимумы.

Ускоренное обтекание активных контуров мимо локальных минимумов.

Рисунок 5.

Неускоренный (в центре) и ускоренный (справа)…

Рисунок 5.

Неускоренный (средний) и ускоренный (правый) результаты активного контура для тех же четырех инициализаций…

Неускоренные (в центре) и ускоренные (справа) результаты активного контура для тех же четырех инициализаций (слева) на изображении сейсмографа. Стоимостные функциональные значения внизу.

Рисунок 6.

(слева): инициализация начального порога…

Рисунок 6.

(слева): начальный порог инициализации шумного квадрата; (в центре): конвергентная сегментация для CP; (справа):…

(слева): инициализация начального порога зашумленного квадрата; (в центре): конвергентная сегментация для CP; (справа): конвергентная сегментация для ускоренного переменного тока.

Рисунок 7.

Реконструкция трех двойных торов с использованием…

Рисунок 7.

Реконструкции трех двойных торов с использованием стереоскопической сегментации методом градиентного спуска. (Слева) тор используется 16…

Три реконструкции двойных торов с использованием стереоскопической сегментации методом градиентного спуска. (Слева) тор использовал 16 изображений и 0 штрафов площади. (Средний) тор использовал 18 изображений и умеренный штраф площади 150. (Справа) тор использовал 18 изображений и большой штраф площади 500. Обратите внимание на умеренную потерю характеристик на финальном изображении.

Рисунок 8.

Сравнение стереоскопической сегментации для…

Рисунок 8.

Сравнение стереоскопической сегментации для градиентного метода PDE и ускоренного метода PDE при…

Рисунок 8.

Сравнение стереоскопической сегментации для градиентного метода УЧП и ускоренного метода УЧП на различных шагах итераций 0, 500, 1000, 2000 и 4000 итераций соответственно. Градиентный метод попадает в ловушку локальных минимизаторов, в данном случае границ тора, и не может формировать дыры без серьезной регуляризации. Обратите внимание, что начальным началом для обоих методов является эллипсоид. Штраф за площадь был зафиксирован на 0, и в этом эксперименте для реконструкции использовалось 16 изображений торов.

Рисунок 9.

(Вверху): вариационный градиентный спуск…

Рисунок 9.

(Вверху): вариационная 3D-реконструкция, основанная на градиентном спуске, оказывается в ловушке локальных минимумов, когда…

Рисунок 9.

(вверху): вариационная 3D-реконструкция, основанная на градиентном спуске, оказывается в ловушке локальных минимумов при сильной регуляризации. (Внизу): ускорение PDE позволяет успешно преодолевать локальные минимизаторы с более высоким штрафом за площадь. Обратите внимание, что среднее время сходимости для ускорения PDE почти в три раза быстрее, чем для градиентного спуска. Итерации приведены внизу, а результаты производительности приведены в таблице 4.

См. это изображение и информацию об авторских правах в PMC

Похожие статьи

• Ускоренные вариационные УЧП для эффективного решения регуляризованных задач обращения.

  Беньямин М., Колдер Дж., Сундарамурти Г., Йеззи А. Беньямин М. и др. J Math Imaging Vis. 2020 янв;62(1):10-36. doi: 10.1007/s10851-019-00910-2. Epub 2019 30 сентября. J Math Imaging Vis. 2020. PMID: 34079176 Бесплатная статья ЧВК.

• Вариационный взгляд на ускоренные методы оптимизации.

  Wibisono A, Wilson AC, Джордан, штат Мичиган. Вибисоно А. и др. Proc Natl Acad Sci U S A. 22 ноября 2016 г .; 113 (47): E7351-E7358. doi: 10.1073/pnas.1614734113. Epub 2016 9 ноября. Proc Natl Acad Sci U S A. 2016. PMID: 27834219 Бесплатная статья ЧВК.

• Ускоренная оптимизация римановых многообразий с помощью дискретных вариационных интеграторов с ограничениями.

  Дюрюиссо В., Леок М. Дюрюиссо В. и др. J Нелинейная наука. 2022;32(4):42. doi: 10.1007/s00332-022-09795-9. Epub 2022 28 апр. J Нелинейная наука. 2022. PMID: 35502199 Бесплатная статья ЧВК.

• Градиентные потоки и методы проксимального разделения: единый взгляд на ускоренную и стохастическую оптимизацию.

  Франса Г., Робинсон Д.П., Видал Р. Франса Г. и др. Phys Rev E. 2021 May; 103 (5-1): 053304. doi: 10.1103/PhysRevE.103.053304. Phys Rev E. 2021. PMID: 34134224

• Алгоритмы неявной регуляризации и импульса в нелинейно параметризованном адаптивном управлении и прогнозировании.

  Боффи Н.М., Слотин Дж.Е. Боффи Н.М. и соавт. Нейронные вычисления. 2021 март; 33 (3): 590-673. doi: 10.1162/neco_a_01360. Epub 2021 Янв 29. Нейронные вычисления. 2021. PMID: 33513321

Посмотреть все похожие статьи

Грантовая поддержка

• R01 HL143350/HL/NHLBI NIH HHS/США

ускоренный, стохастический, асинхронный, распределенный Теория вычислений в контексте их продолжающейся в настоящее время серии Вычислительные задачи в машине Обучение.

\начало{уравнение} \label{eq:nesterov}\tag{1} \left \lbrace \begin{array}{lll} y_{k + 1} & = & x_{k} — \beta \nabla f (x_{k})\\
x_{k + 1} & = & (1 — \lambda _{k}) y_{k + 1} + \lambda _{k} y_{k} . \конец{массив}\право. \end{equation}

Обратите внимание, что на самом деле это не градиентный спуск, поскольку импульс сделает траектория в какой-то момент отклоняется от «самого крутого склона».

Градиентный спуск — это дискретизация градиентного потока:

\[ \dot{X}_{t} = — \nabla f (X_{t}) . \]

Метод Нестерова представляет собой дискретизацию ОДУ ²

\begin{equation} \label{eq:su-boyd-candes-ode}\tag{2} \ddot{X}_{t} + \frac{3}{t} \dot{X}_{t} + \nabla f (X_{t}) = 0. \end{уравнение}

Вопрос 1: Эти ОДУ получаются путем принятия непрерывных ограничений по времени. Является есть ли более глубокий порождающий механизм?

Лагранжева точка зрения

Для оптимизации целевой функции $f$ определите 9{\beta _{t}} f (x)$ как потенциальная энергия, яму которой мы идут вниз. Выбор $h$ будет зависеть от геометрии задачи, то есть на пространстве, где происходит минимизация.

Масштабирующие функции $\alpha _{t}, \beta _{t}, \gamma _{t}$ на самом деле исправлено определенными идеальными условиями масштабирования уменьшением их до одного Эффективная степень свободы. Это ограничение было разработано, чтобы получить желаемые показатели ниже, но все пространство параметров не исследовано. 9{- 1} \nabla f (X_{t}) = 0. \]

При $p = 2$ получается (2). Подстановка различных значений $p$ дает другие методы (например, ускоренный кубически-регуляризованный метод Ньютона для $p = 3$). Интересно, что $\mathcal{L}$ является ковариантным оператором : a репараметризация времени (в частности изменение $p$) не меняет путь решения .

При этих предположениях у нас есть оптимальный способ оптимизации: существует конкретный путь и ускорение просто меняют скорость, с которой вы двигаетесь вдоль него.

Обратите внимание, что это не свойство градиентного потока: изменения репараметризации путь. В общем случае он будет отличаться от полученного из (4).

Вопрос: (аудитория, «Нахди»?) Можно ли ввести новые параметры в основной ODE (или изменить текущие) для интерполяции в что-то среднее между нестеровскими методами и градиентным потоком?

Ответ таков: действительно, весь диапазон $\alpha _{t}, \beta _{t}, \gamma_{t}$ не исчерпан и “ мы можем восстановить другие алгоритмы исследуя [это] ».

Дискретизация уравнения E-L (1)

(с сохранением устойчивости и скорости сходимости). Первое, что нужно думает о том, чтобы свести уравнение 2-го порядка к системе 1-го порядка и применить например схема Эйлера для получения алгоритма. Проблема в том, что метод нестабильный! (и это потеряло скорость)

Нестабильность обычных методов для мастера ОДУ.

Тогда можно попробовать Рунге-Кутту или что-то еще: все они теряют стабильность и оценивать. Группа Джордана увидела два подхода к решению этой проблемы: «реконструировать метод последовательности оценок Нестерова», интерпретируя его как метод дискретизации или использовать симплектическое интегрирование (см. ниже). Для во-первых, можно восстановить скорость оракула, увеличив предположения на $f$: 9р} \справа) . \]

Но, как правило, не требуется принимать на себя эти дополнительные условия на $\nabla f$ (липшицевы $p — 1$ производные).

Дискретизация уравнения Э-Л (2): симплектическое интегрирование

Симплектическое интегрирование это метод численного интегрирования, который сохраняет такие величины, как энергия и импульс в (зависящей от времени) гамильтоновой структуре. ⁵ Взяв Преобразование Лежандра (также известное как сопряженное Фенхеля) скорости и времени получает импульс и энергию соответственно и может написать гамильтониан, который в основном имитирует лагранжиан, который у нас был (он имеет вид (3) по модулю констант и знаки). Затем решают уравнения Гамильтона в фазовом пространстве с дискретизация, которая рассматривает и сохраняет определенный тензор локального объема / дифференциальная форма на пути интегрирования.

Чем это интересно в нашем сеттинге? Дискретность, наблюдаемая для Лагранжева формулировка страдает высокой чувствительностью к размеру шага и нарастание импульса, которое ухудшает производительность вблизи оптимума. Гамильтониан перспектива дает эквивалентные уравнения, симплектическое интегрирование которых должно решить эти проблемы и добиться более высоких скоростей без дополнительных предположений: сохранение импульса кажется ключевым.

Сравнение лагранжевых и симплектических интеграторов.

Два возможных места для исследования:

• Невыпуклая установка: описанная структура также может быть применена.
• Стохастические уравнения: вероятно, также будет существовать «оптимальный способ диффузные» в СДУ, полученные из некоторого уравнения типа Фокера-Планка.

1. Поскольку мы находимся в гладкой выпуклой среде, существует глобальный минимум: если вы его знаете, то вы тривиально достигаете его за один шаг. Помимо этого бесполезного случая, если есть производные более высокого порядка, то методы более высокого порядка обеспечивают более высокую скорость сходимости и так далее. По этой причине необходимо в некотором смысле ограничить определение оптимальности. С этой целью было введено понятие оракула: оракул — это сущность, которая «отвечает» на вопросы схемы оптимизации об оптимизируемой функции (например, каково значение $\nabla f$ в точке $x_{k}$). ?), внутри модели задачи (т.е. представляет то, что известно методу). Это приводит к определению класса 92)$. См., например. Вводные лекции по выпуклой оптимизации — базовый курс, Нестеров, Ю. (2004) , Глава 1 для получения дополнительной информации об оракулах и §2. 1.2 для предыдущих утверждений, первоначально доказанных в Метод решения задачи выпуклого программирования со скоростью сходимости O (1/k2), Нестеров, Ю. (1983) . ^⇧
2. Дифференциальное уравнение для моделирования метода ускоренного градиента Нестерова: теория и идеи, Су, В. , Бойд, С. , Кандес, Э. (2016) напишите уравнение конечных разностей для (1), возьмите предел, когда размер шага стремится к нулю, и найдите непрерывное уравнение. ^⇧
3. Обратите внимание, что это имеет грубую форму затухающего осциллятора с дополнительным «геометрическим членом», включающим гессиан производящей функции расстояния, оцениваемой как «$X$ плюс скорость» (что дает ускорение).

   Comments |0|

   Cancel

   Remember me

   * Name:

   * @ Email:

   Website:

    
   Legend

   *) Required fields are marked
   **) You may use these HTML tags and attributes: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>
   
   Category: Разное